This can be reached only by an efficient model describing the behavior of the disease over time with some parameters to depend on. So, for modeling the infections of COVID-19 disease, we need to use the Kermack-McKendrick SIR Model, in which they model the total population classified into three categories S, I, and R: where Susceptible (S), are healthy individuals that are free of the disease but are susceptible to the infection by the Infectious (I), Infectious are the ones who tested positive for the disease, and then for simplicity after a period of time considered Recovered (R), as it’s assumed that they gained permanent immunity.

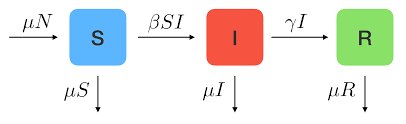
The SIR model can provide us with insights and predictions of the spread of the virus in communities that the recorded data alone cannot. And it’s represented by a few ODEs, including 2 main parameters which are the infectious rate (β) and the recovery rate (γ) .

The assumptions made are that the Population (N) is a homogeneous mix of the infected I and susceptible S, where mere contact causes the spread of the disease, and for simplicity, the population is placed in a relatively small confined space, there are no immigrants or births in the population. Also assuming that once a person is Recovered R, they are no longer in the scope of the population being studied because they won’t get reinfected (or are dead). The infectious people are assumed to be spreading the disease for a constant time t before they are removed from the pool and considered Recovered (i.e there’s a fixed infection rate per day and fixed recovery time). In this particular scenario, the number of susceptible people would decay monotonically over time to zero.

Learn more about SIR and compartmental models in epidemiology